Code Signing and Authentication

A critical piece of Java's security model is the support for authentication introduced in Java 1.1 in the java.security package and its subpackages. The authentication capabilities expand your ability to establish multiple security policies by enabling you to implement a sandbox that varies depending upon who vouched for the code. Authentication allows you to verify that a set of class files was blessed as trustworthy by some party, and that the class files were not altered en route to your virtual machine. Thus, to the extent you trust the party who vouched for the code, you can ease the restrictions placed on the code by the sandbox. You can establish different security restrictions for code that is signed by different parties.

To vouch for, or sign, a piece of code, you must first generate a public/private key pair. You should keep the private key private, but can make the public key public. At the very least, you must somehow get the public key to anyone who wants to establish a security policy based on your signature. (As will be illustrated later in this section, distributing public keys is not necessarily as easy as it may seem.) Once you have a public/private key pair, you must place the class files and any other files you want to sign into a JAR file. You then use a tool, such as jarsigner from the 1.2 SDK, to sign the entire JAR file. The signer tool will first perform a one-way hash calculation on the contents of the JAR file to generate a hash. The tool will then sign the hash with your private key, and add the signed hash to the JAR file. The signed hash represents your digital signature of the contents of the JAR file. When you distribute the JAR file that contains the signed hash, anyone with your public key can verify two things about the JAR file: the JAR file was indeed signed by you, and the contents of the JAR file were not in any way altered since you attached your signature.

The first step in the digital signing process is the one-way hash calculation, which takes a big number as input and generates a small number, called the hash. In the case of a JAR file, the big-number input to the calculation is the stream of bytes that make up the contents of the JAR file. The one-way hash calculation is called "one-way" because given just the hash (the small number), it is impossible to calculate the input (the big number). In other words, the hash value doesn't contain enough information about the input to enable the input to be regenerated from the hash. The calculation goes just one way, from big to small, from input to hash.

The hash, which is also called a message digest, serves as a kind of "fingerprint" for the input. Although different inputs can produce the same hash, the hash is considered unique enough in practice to represent the input from which it was generated. Much like a fingerprint can be used to identify the individual who made the fingerprint, a hash can be used to identify the input that caused the one-way hash algorithm to produce the hash. The hash is used during the authentication process to verify that the input is identical to the input that produced the original hash, in other words, that the input was not changed en route to its destination.

Given that it is impossible to reconstruct the input given just the hash, a hash is only useful if the input is also available. Thus, you normally transmit both input and hash together. By themselves, the combination of an input and its hash is not secure, however, because even an extremely unimaginative cracker could simply replace both the input and the hash. To prevent this scenario, you encrypt the hash with your private key before sending it. The reason you encrypt the hash rather than simply encrypting the entire JAR file is that private key encryption is a time-consuming process. It is in general much faster to calculate a one-way hash from the JAR file contents and encrypt the hash with a private key than it is to encrypt the entire JAR file with the private key. A cracker will only be able to replace both an input and encrypted hash if the cracker has your private key, which you are supposed to keep secret. Thus, the combination of input and encrypted hash is more frustrating to a potential cracker than the mere combination of input and hash because, in theory, the cracker doesn't have your private key.

Anything encrypted with your private key can be decrypted with your public key. Public/private key pairs have the characteristic that it is prohibitively difficult given just the public key to generate the private key. If you can keep your private key out the hands of crackers, therefore, their best option is to try and replace the input with a different input that yields the same hash value. If the cracker wishes to replace one class file in your JAR file with a different class file that performs some devious act, for example, the odds are extremely high that the revised JAR file (the one that contains the devious class file) will produce a different hash. But the cracker could add random data to the JAR file until the one-way hash calculation on the altered JAR file produces the same hash value as the original. If the cracker can produce such an alternative input -- one that both helps the cracker achieve his or her nefarious goals and generates the same hash as your original input -- the cracker would not need your private key. Because the cracker's input generates the same hash value as your original input, and you have already signed that hash value with your private key, the cracker can simply place your signed hash in a JAR file with his or her input. What's to prevent a cracker from taking this approach? Unfortunately for the cracker, such an approach would likely take too much time to be feasible.

Because one-way hash algorithms generate a small number (the message digest or hash) from a big number (the input), different inputs can produce the same hash. One-way hash algorithms tend to spread out the inputs that produce the same hash sufficiently randomly that the likelihood of getting the same hash value depends primarily on the size of the hash. For example, if you use a hash value that is 8 bits wide, your one-way hash algorithm will have only 256 unique hash values from which to choose. If you have a JAR file that produces the hash value 100 and you start calculating the 8 bit hash with this algorithm on other JAR files, you shouldn't be surprised if every 256 times or so you get the hash value 100. The more bits contained in the hash, of course, the less often the algorithm will produce the same hash. In practice, 64- and 128-bit hash values are common, which are considered large enough to render the process of finding a different input that produces the same hash computationally infeasible. The main barrier preventing a cracker from replacing your benevolent input with a malicious input that serves the cracker's evil purposes and produces the same hash, therefore, is the time and resources the cracker would have to devote to searching for that malicious input.

The last step in the digital signing process, after you have generated the hash value and encrypted it with your private key, is to add the encrypted hash value to the same JAR file that contains the files from which you generated the hash value originally. A signed JAR file, therefore, contains the input -- the class and data files you wanted to vouch for -- plus the hash value (generated from the input) encrypted with your private key. The encrypted hash represents your digital signature of the class and data files contained in the same JAR file. The process of signing a JAR file is shown graphically in Figure 3-3.

Figure 3-3. Digitally signing a JAR file.

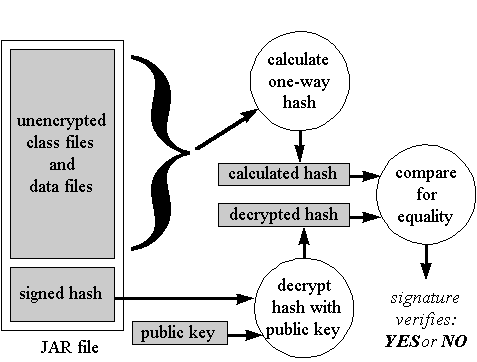
To authenticate a JAR file that you have purportedly signed, the recipient must decrypt the signed hash with your public key. The result should be equal to the original hash that you calculated on the contents of the JAR file. To verify that the JAR file contents were not changed since you signed them, the recipient simply applies the one-way hash algorithm on the contents of the JAR file, just as you did during the signing process. (Remember you never encrypted contents of the JAR file, so anyone can see them. You only added a digital signature to the JAR file.) If the hash value generated by the algorithm matches the decrypted hash value, the recipient concludes that you did indeed vouch for this JAR file and that the contents of the JAR file did not change since you added your signature. The code contained in the JAR file can be placed inside a relaxed sandbox that represents the trust the recipient places in your signature. The process of verifying a digitally signed JAR file is shown in Figure 3-4.

Figure 3-4. Authenticating a digitally signed JAR file.

Although the authentication technology first introduced in Java version 1.1 is firmly founded in reliable mathematics, the math doesn't solve every problem. In fact, several questions are raised by Java's authentication technology. For example, the authentication technology says nothing about who you should trust, and to what extent you should trust them. To what extent do you trust some small company that you've never heard of? To what extent do you trust a big company whose name is a household word? To what extent do you trust a different department in your own company? What are the chances that any particular company (or department) has a rogue employee who managed to slip a time bomb into a JAR file the company signed? No cryptographic algorithm can answer these questions for you.

Another security issue stems from the assumption inherent in the authentication technology that private keys will be kept under lock and, well, key. If private keys are not kept private, the entire authentication scheme is reduced to strenuous mathematical activity that is not only ineffective, but dangerous, because it can give a false sense of security. You are responsible for keeping your own private keys private. You can only hope that any entity on whose signature authority you grant code access to your system has kept their private keys private. For any party, establishing a key management scheme that prevents private keys from being leaked (remember those rogue employees?) can be a challenging task.

Another question raised by the technology involves the distribution of public keys. Although it may seem surprising at first, the assumption inherent in the authentication technology that public keys will be made public creates some security issues of its own. For example, imagine you want to relax your sandbox for code vouched for by a guy named Evan. To do so, you need Evan's public key. But how exactly do you get his public key? If you know Evan personally, you can invite him over for coffee and ask him to bring his public key so he can give it to you in person. But what if you don't know Evan personally? You might think you could simply visit Evan's web site and grab his public key off a web page. Or alternatively, perhaps you could phone Evan and ask him to send you his public key in an e-mail. Evan should have no problem sending you, a stranger, his public key, because public keys after all are designed to be public. Evan doesn't need to worry about who gets his public key. He could hire a biplane to write his public key on the sky over Silicon Valley and still feel confident he was operating within the rules delineated by Java's authentication technology. So what's the problem? The problem is that even though Evan doesn't need to worry about your identity when he sends you his public key, you need to worry about his. Evan will be happy to send you his public key, but how do you know that the public key you receive is really the one that Evan sent?

The difficulty of public key distribution is that no matter what the means of communication, the message -- the public key -- could potentially be tampered with in transit. When you visit Evan's web page, it is possible that the web page is intercepted and changed en route to your browser, perhaps by Dastardly Doug, a cracker of international repute. When you think you are copying Evan's public key off his web page, you could actually be copying Dastardly Doug's. Doug could also have intercepted Evan's e-mail and replaced Evan's beneficent public key with his own dastardly public key. Doug could even have donned one of his many clever disguises and piloted the biplane high above Silicon Valley, inscribing his public key among the clouds in place of Evan's. If Doug can successfully replace Evan's public key with his own, Doug can pretend to be Evan and take advantage of the trust you place in Evan's signature to break into your system.

But wait a minute, isn't the difficulty of public key distribution just another authentication problem, the kind of problem the authentication technology itself is designed to address? In fact it is, and by turning authentication back on itself, Evan can make it far more difficult for Dastardly Doug to replace Evan's public key with his own.

To address the difficulties of public key distribution, several certificate authorities have been established for the purpose of vouching for public keys. Evan, for example, could go to a certificate authority and present his credentials (birth certificate, drivers license, passport, and so on) and his public key. Once convinced that Evan is who he says he is, the certificate authority would sign Evan's public key with the certificate authority's private key. The resulting sequence of numbers is called a certificate. Instead of distributing his public key, then, Evan would distribute his certificate.

You could grab Evan's certificate off of his web page, out of an e-mail, or via any other unsecured communications medium. When you get the certificate, you decrypt it with the certificate authority's public key and are rewarded with Evan's public key. The certificate scheme makes it much less likely that Doug will be able to swap his public key for Evan's because to do so, Doug would need the certificate authority's private key.

Although certificates improve the public key distribution situation immensely, some issues still remain. First of all, how exactly to you get the certificate authority's public key? You need this public key to authenticate the public keys of anyone else. Well, if you know any employees of the certificate authority personally, you could invite them over for coffee and ask them to bring their public key to give to you in person. But what if you don't know any employees of the certificate authority personally? And then there is the nagging question: why should you trust the certificate authority? A certificate authority can pretend to be anyone. Isn't a certificate authority just as susceptible as the next company to the vagaries of rogue employees?

Despite all these issues, the code signing capabilities introduced in Java 1.1 generally offer you enough security to enable you to relax your sandbox when you need to. Although the authentication technology doesn't eliminate all risk associated with relaxing the sandbox, it can help minimize the risks. Security is a tradeoff between cost and risk: the lower the security risk, the higher the cost of security. You must weigh the costs associated with any computer or network security strategy against the costs of the theft or destruction of the information or computing resources being protected. The nature of your computer or network security strategy should be shaped by the value of the assets you are trying to protect. Java's authentication technology is a useful tool that, in concert with Java's sandbox, can help you manage the costs and risks of running network-mobile code on your systems.